
モンテッソーリ教育について
モンテッソーリ教育とは
モンテッソーリ教育は、イタリア初の女性医学博士であるマリア・モンテッソーリ博士(1870年 - 1952年)によって確立された幼児教育法です。博士は特に数学の能力に秀でており、その数学力を基礎とし、医学のみならず実験心理学や教育学等の研究にも没頭しました。そのような多様な学問的バックグラウンドを持ちつつ、自然科学者としての客観的な視点により、子供たちの観察を通じたファクトベースの教育法を構築しました。いまから1世紀近く前に構築された当教育法は、現代の大脳生理学や心理学、教育学などにより、多面的にその有効性が証明されています。
モンテッソーリ教育の特徴
モンテッソーリ教育は様々な要素が有機的に結合しているため、その特徴について一言で言い表すことは困難です。あえて申し上げると、「人間としての知性の自発性」を基礎にした教育法です。これにより、科学的思考、主体性、没頭力が養われると考えられます。モンテッソーリ教育では人間としての知的好奇心を誘起することで、子供が主体性を持って没頭し成長するための教具や環境がデザインされています。実際、敏感期(子供が何かに強く興味を持つ一定の時期)をベースに体系化された5分野(日常生活の練習・感覚・算数・言語・文化教育)があり、様々な教具や用具が用意されています。

人間としての知性
子供が夢中になってあるモノを集めたり、比較したり、組み合わせたりしている場面に遭遇したことはないでしょうか。博士はこのような行動を「区別する働き」と称し、知性をもつ人間に特徴的な行動であると考えました。実際、このような行動はいわゆる「分析・統合」であり、子供特有のものではなく、科学者やビジネスパーソンにとっても必須の科学的思考アプローチであることはよく知られています。子供の行動を観察していると、子供は生まれながらに「ハカセ=Doctor」のような存在であると気付かされます。

自発性
子供が自らの興味に従い、内発的動機づけにより自発的に行動した場合、大人が声をかけても気付かないくらい集中した「没頭」状態になることがあります。没頭できることは、幼少期の学習や成長のみならず、ビジネスにおいても重要です。この状態になるには「真剣な興味」をもつことが必要だと、米国サドベリーバレー・スクールの創始者グリーンバーグにより指摘されています。このことは、博士が定義した「敏感期」の概念とも類似しており、この敏感期の出現を大人が見極めた上で、ヒトやモノを含めた適切な環境を準備する必要があります。
幼少期にモンテッソーリ教育を受けた著名人
世界140以上もの国に広まっているモンテッソーリ教育では、世界をリードする著名人を多数も輩出しています。一例ですが、Googleの共同創業者であるセルゲイ・ブリンとラリー・ペイジ、Amazon創業者のジェフ・ベゾス、Facebook創業者のマーク・ザッカーバーグ、経営学者のピータードラッカー、棋士の藤井聡太などが幼少期にモンテッソーリ教育を受けていたと言われています。

Dr.Childの教育理念
自ら育つ子どもの育成に貢献します
どのような時代でも生き抜くことができる人を育てるため、Dr.Childは「自ら育つ子ども」の育成をサポートします。
自立し、成長していく姿勢は、大人になってからも必要となります。
自ら育つためには、以下の4つの力が特に重要であると考えています。
①好奇心
自ら育つ上では、まず自分を取り囲む環境や物事に対して「好奇心(興味)」を持つことが必要です。周囲の物事に対して好奇心を持って接することで、子どもながらに自分の意思で問いや目標を設定し、行動へつなげることができます。好奇心が学習や成長、選択判断の出発点となります。
②粘り強く集中する力
成長や学習においては、抱いた好奇心や目標に対する行動を継続させること、つまり「粘り強く集中する力」が必要となります。このような力を育む上では、子どもが安心して集中できる環境のもとで、失敗を恐れず目標に挑戦する経験を積むことが大切です。
③考える力
「なぜ?」や「どうすればよい?」といった、好奇心に基づいて子どもが自ら設定した問いに答えるためには、分析力・統合力・論理的思考力といった「考える力」も必要となります。これらは、自分の意図を表現するためのプレゼンテーションスキルや、問題解決する上で基本となる能力であり、大人になってからも必要となる能力です。
④自尊感情
どんなに小さなスケールであっても、子どもにとって目標を達成できることは非常に嬉しいものです。Dr.Childでは子供に寄り添い、一緒に達成感や充実感を共有します。そこから得られる「自尊感情」ならびにプロセス中で獲得したスキルは、また新たな興味を湧かせるモチベーションとなり、学習や成長へ好循環をもたらします。

Dr.Childの特徴・コンセプト
モンテッソーリ教育と算数・数学教育を組み合わせることで
認知能力と非認知能力をバランスよく養い、自ら育つ子どもを育みます

自立心・好奇心・集中力を育む
Dr.Childではモンテッソーリ教育の基本精神に則り、子どもの自発性を尊重する教育を実践することで自立心を育みます。またモンテッソーリ教育は、敏感期に合わせ子どもの興味を引くようにデザインされているため、活動を通じて自然と知的好奇心の育成にも繋がります。加えて、Dr.Childでは子どもたちの活動を阻害しない環境を整備しつつ、サポートを行うことも大切に考えているため、子どもたちは安心して集中する経験も積むことが出来ます。

数学教育により考える力を育む
モンテッソーリの感覚・算数教育は、その系統性や教具を用いた教育により、数学的基盤の構築にも効果を発揮します。モンテッソーリ活動にて体験的に得た数学的発見や知的好奇心をより一層深化させるため、Dr.Childでは理学博士監修の下、独自に数学教育を並行して行います。数学は計算能力といった認知能力に加え、論理的思考力といった考える力を育むのにも適しています。これらの組み合わせにより、ペーパーや暗記中心型の教育では得られない数学に対する深い理解と考える力を育みます。

個々の発達を尊重した教育
個々の子どもの発達に合わせたモンテッソーリ教育ならびに算数・数学教育を行うことで、子どもたちの成長意欲をサポートしつつ効果的な教育を実践します。したがって、画一的な集団指導や、教師からの強制的な指導ではなく、子どもたちを中心とした教育となります。また、モンテッソーリ教具やオリジナルの数学教具などの具体物を用い、手を動かしながら学ぶことで、子どもたちにとって楽しく吸収しやすい教育を目指しています。

自育サイクルの習慣化
幼児教室や塾で学ぶ時間よりも、当然ながらご家庭で過ごす時間の方が多くなります。家庭での食事、散歩、買い物など、日常生活の様々な場面においては、子どもの学習や成長を促す機会や題材が豊富に存在しています。Dr.Childでは、日常生活も意識した教育を行うことで、教室で学ぶ時間だけでなく、それ以外の大部分を占める時間においても、子どもが物事に興味をもって自育のサイクルを回せるような教育を目指しております。
幼児期からの数学教育について
なぜ幼児期からの数学教育が重要なのか?

認知能力と非認知能力をバランスよく育成できる
「認知能力」とは読み書きや計算能力など、従来の学力テストで数値化できる能力のことを指します。一方で、思考力・判断力・表現力などの見えにくい学力や、好奇心・意欲・自己肯定感といった客観的に見えない力のことを「非認知能力」と呼びます。実はこの非認知能力を伸ばすことで認知能力にもプラスの影響を与えるため、結果的に学力も伸びていくと考えられています。幼児期から数学を学ぶことにより、論理的思考力といった基本的な考える力に加え、足し算などの計算能力や読解力(国語力)もゆっくりと育むことができます。Dr.Childでは子どもの興味を重視しつつ、手を動かしたり具体物に触れながら数学を学べる環境を整えることで、認知能力と非認知能力をバランスよく育成します。

小学校算数教育への接続
数学は、他の分野と比較し単元の前後関係が明確です。つまり、ある単元の理解をベースに次の単元に接続する、系統立った構造となっています。そのため、ある単元でつまづくと後続の理解が難しくなり、苦手意識から数学嫌いを引き起こします。このような中、小学校入学と同時に本格的な数学教育がスタートするため、入学前までの数学的準備が不足している場合はつまづく可能性が高いです。したがって、幼少期から数学に親しむことが必要です。

人生の選択肢を拡げる
数学が苦手でも、数学が不要な環境を選択すれば不自由なく生活できるのは確かですが、選択肢の幅を狭めてしまっているのも事実です。実際、小学生時には医師やエンジニア、科学者など、数学を駆使する理系職を志望する傾向にありますが、高校段階になると「数学が苦手だから」後ろ向きに文系を選択するケースも少なくありません。数学が苦手で、幼少期に抱いていた夢を諦めてしまうこともあると考えられます。
なぜモンテッソーリ教育が幼児期の数学教育に効果的なのか?
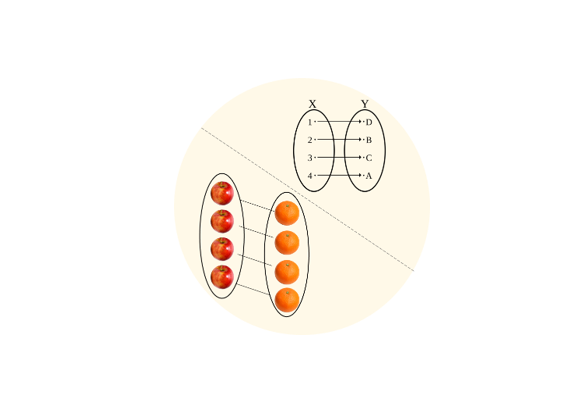
感覚教育による数学的基盤の形成
代数学や幾何学、解析学などの現代数学は、集合論を基礎として成立しており、集合論の理解が必須であると言っても過言ではありません。集合論とは、あるものの集まりを考え、そこから対応や比較などの数学的操作をもとに各種理論を展開する分野です。モンテッソーリ教育では、算術や幾何などを扱う算数教育の前に感覚教育を行いますが、実は感覚教育の教具は集合論の基本概念を体感できるようデザインされているため、子供たちは楽しみながら数学的基盤を形成していくことができるのです。

系統性ならびに抽象概念の具体化
算数・数学は日常生活において身近な存在でありながら抽象性が高く、また言語教育等と比べ、家庭内教育では対応し辛い側面があります。実際、数に関する概念を理解するためには、一定のプロセスが必要です。つまり、計算方法の習得前に、数字・数詞・数量(離散量や連続量)の関係性を把握し、その上で基数性や序数性などの数的性質を理解することが重要です。モンテッソーリの算数教育では、このプロセスと同様の系統性が構築されており、また教具という具体物を用いることで抽象概念が理解しやすくなっております。





