【数学コラム】積分と図形

こんにちは、Dr.Childです。

Dr.Childの数学レッスンでは、はさみとのりを使った遊びも実践しており、一部紹介させて頂きます。

皆さんは高校数学で積分を学びましたでしょうか？

微分・積分と聞くと、それだけでアレルギーが出る方もいらっしゃいますよね。

高校では、積分は微分の逆操作と機械的に学ぶことが多いためとっつきにくく、しかも何に応用されるかも分からないまま、期末テストのためだけに勉強した方も少なくないのではないでしょうか？

しかし、積分はその本質が「面積」であることが分かれば理解が進みやすくなりますし、多方面でも応用することができます！

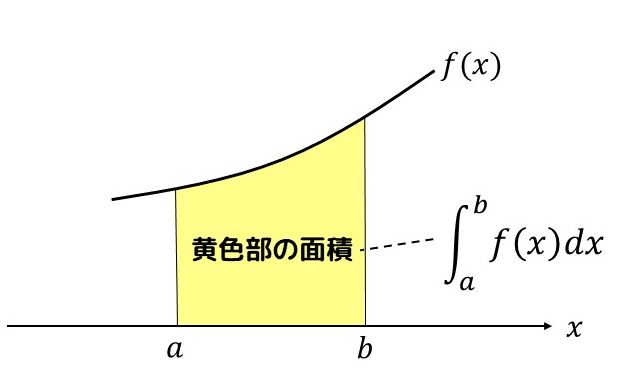
積分はある曲線で囲まれた、ヘンテコな図形の面積でも求めることができる優れものですが、これを視覚的に理解するための方法としては、その図形を短冊を並べて埋めつくしていくやり方があります（区分求積法と言います）。

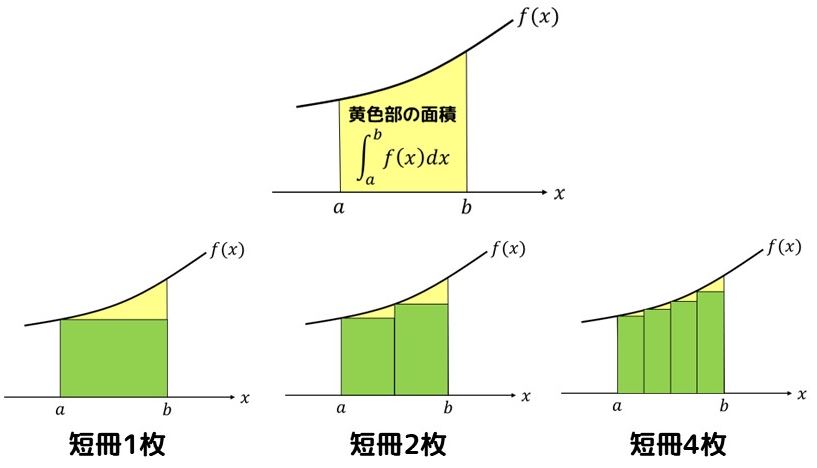
実は上図のように短冊を細くすればするほど元の図形に近づくように並べられるため、短冊の面積の和が、積分で得られた値に近似できることが分かります（一枚一枚の短冊は長方形なので、簡単に面積が求まります）。

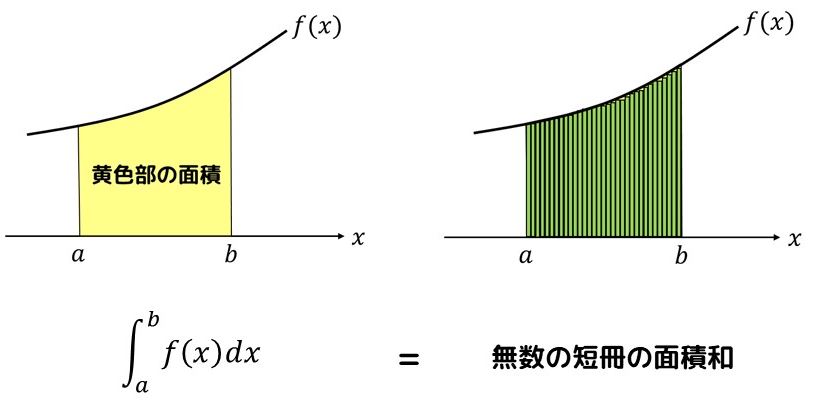
したがって、積分は限りなく細い短冊たちの面積和であることが分かりますが、この感覚とイメージを持てていると物理学などへの応用にも活かせることができます。

実はこのような図形の分割については、モンテッソーリの構成三角形のお仕事で学びます。そこでは元の図形をぴったり再現できる分割操作のみを学びますが、一方で子どもたちは図形の等価性などを感覚的に学ぶことができます。

Dr.Childではその応用としてヘンテコな図形も短冊を使って近似できることも、はさみとのりを使って体験的に学びます（写真のような方法で短冊を無数に増やしていくと、実際に三角形の面積が正確に求まります。当然ですが積分計算は教えていません）。

いつか積分を習った際に、「Dr.Childで小さいときにやったことあるな」と思い出してくれると嬉しいですね！