【教育法】子どもの数学的興味と思考力を伸ばす方略
こんにちは、Dr.Childです。
今回は、Dr.Childで実践している「子どもの数学的興味と思考力を伸ばすステップ」をご紹介したいと思います。
なお、当ステップにはDr.Childのみならず、ご家庭で過ごす時間も重要であることを示しております。
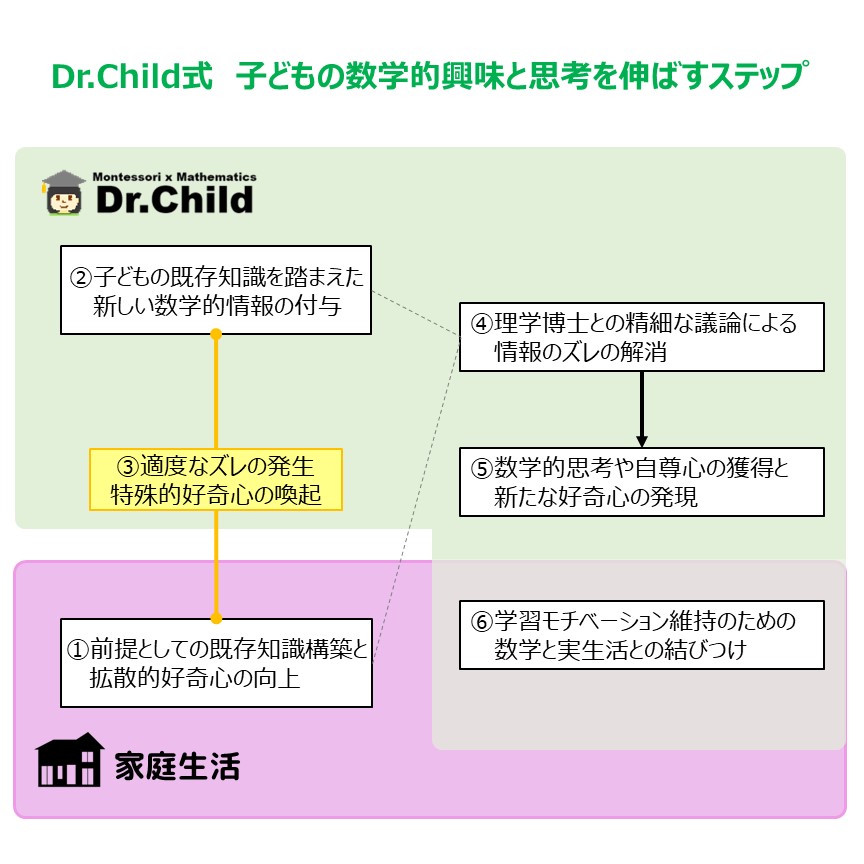
【①前提としての既存知識構築と拡散的好奇心の向上】
こちらは、②以降で示されているプロセスに進む上での前提の一つとなります。つまり、既存知識がないとそもそも新たな情報が与えられた際に情報のズレが生じないため、子どもの内から遊びなどを通じて幅広い知識や経験を蓄積しておくことが必要となります。ここで拡散的好奇心とは、新しく多様な知的情報を探索する原動力となるものです。もちろん、Dr.Childでもこれらを伸ばすことを実践しておりますが、やはりご家庭での生活や遊びを通した経験に勝るものはないと考えております。
【②子どもの既存知識を踏まえた新しい数学的情報の付与】
ステップ②以降はDr.Childで行うものになります。まず、教室での子どもの行動やモンテッソーリ教具への関心を観察することで、備わっている数学的な既存知識を確認します。その上で、数学に関連した新しい情報をモンテッソーリ活動や数学レッスンにおいて講師から提示します。
【③適度な情報のズレの発生と特殊的好奇心の喚起】
簡単すぎず、また難しすぎないレベルの新しい情報を提示した場合、子どもには特殊的好奇心が発生します。特殊的好奇心とは、現れた情報のズレの原因を解消するために、持続的かつ積極的に情報を探索する原動力となるものです。また、このことが子どもの知的好奇心も促進します。
【④理学博士との議論によるズレの解消】
子どもたちが抱いた疑問や導いた答えに対し、専門性の高い理学博士の講師が子どもたちと対等に、分かりやすくかつ正確な言葉と論理でもって議論することでズレの解消を行います。
【⑤数学的思考の獲得と新たな好奇心の発現】
ズレが解決できたことに対する自尊心や自己肯定感に加え、議論の過程において数学的な考え方を身につけることができます。また、さらに広く深く知りたいという新たな好奇心にも繋がります。
【⑥学習モチベーション維持のための数学と実生活との結びつけ】
子どもたちに生まれた新たな好奇心や学習モチベーションを維持するため、Dr.Childで学んだ数学的思考や知識と、実生活での応用とを結びつけます。これにより、ご家庭でも子ども自ら興味を持って進んで学ぶようになります(教室以外でも学びの場を得ることになります)。
このようにして、子どもたちの数学的興味と思考を伸ばすことを心がけております。詳しくは講師にお尋ね下さい。
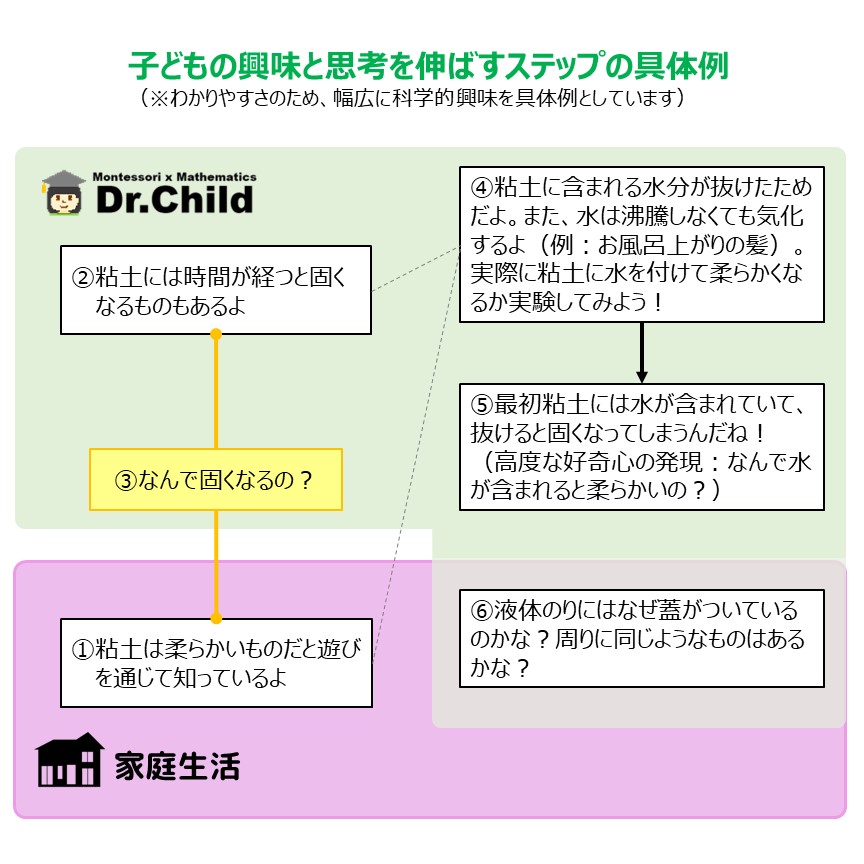
■具体例