【算数コラム】基数性と序数性

3/3はひな祭りでしたね。
皆さま、飾り付けなど大変だったかと思いますが、楽しめましたでしょうか？

今回は数のもつ基数性と序数性について話したいと思います。

数の概念には、何個や何gといった量的側面を表わす「基数性」と、順番といった順序的側面を表わす「序数性」があります。

基数性

ある集合の個数を数える場合、集合の各要素に対し、数を1対1で正確に対応させていく必要があります。そして、最後に割り当てられた数がその個数になります。このように、基数性は量を表す数の性質のことを指します。
（例：かごにみかんが5個あるとします。一つ一つのみかんに対し、数（イチ、ニ、サン、シ、ゴ）を1対1に対応させることで数えあげることができます。最後の数「ゴ」がみかんの個数に対応します）

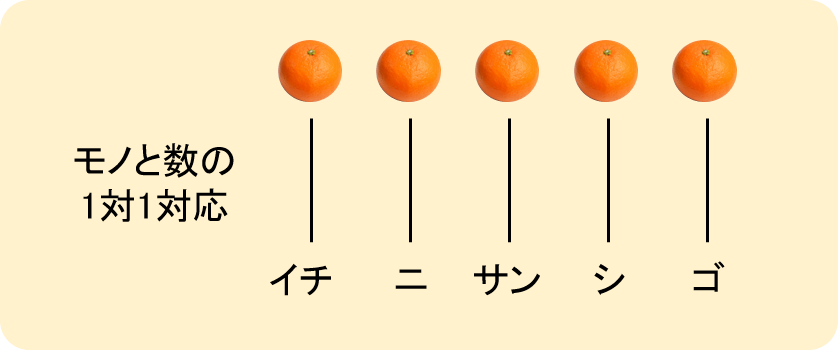
また、基数性は数の量的感覚を表すものですので、これが捉えられることで数（分離量や連続量）の大まかな量を把握したり、大小を瞬時に判断することができます。
（例：50 と80はどちらが大きい？60cmのテープは30cmのテープの何個分？）

基数性の力が弱いと「イチ、ニ、サン、シ、ゴ…」と唱えられるけど、指定された集合の個数を答えられなかったり、数量を大まかに把握したり数の大小を瞬時に比較することが難しくなります。

序数性

序数性は、上から何段目とか列の前から何番目といったように、順序的側面を表す数の性質のことを指します。

序数性が弱いと、「7の次は？」と子どもに聞くとまた1から数え直したり、自分の座席が前から何番目かを正しく答えることが難しくなります。

一方で、序数性が身についている子どもは、上記の問いに対してスムーズに答えることができます。

この違いは、数が系列であって順序を表していることを理解しているかどうかに依ります。

これを、心的数直線が形成されているという研究者もいます。

数が順序よく整列する数直線が頭にイメージできれば、序数性も理解しやすくなるという考え方です。

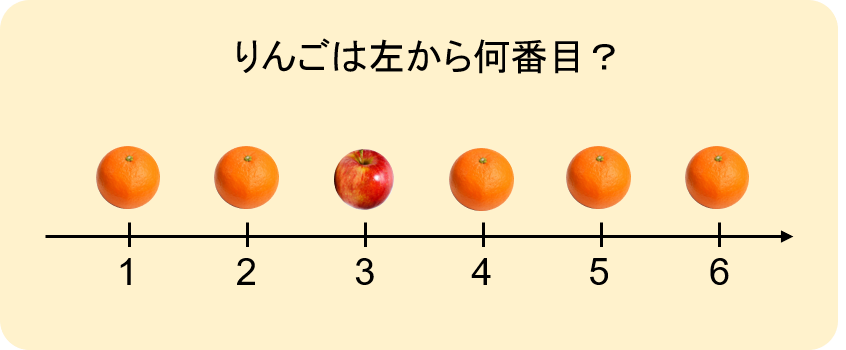
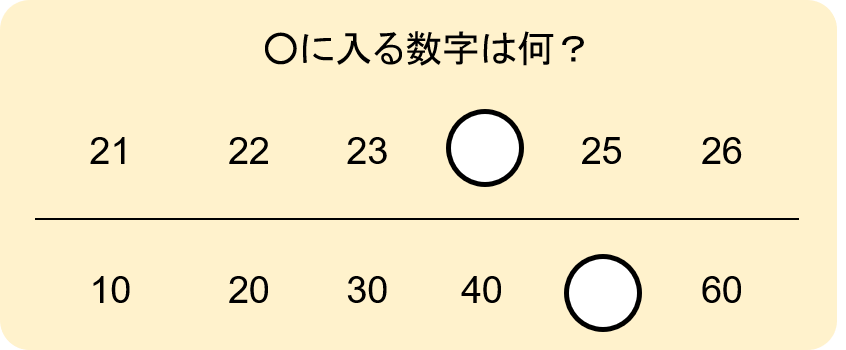
私たちの幼児教室ではモンテッソーリ教具やオリジナルの教具を通じて、このような数の概念も学びます。
お子様の理解度を確認しつつ、まずは具体物を用いて数の概念をイメージしやすい形にしてから学ぶようにしています。

練習問題

今回、ひな祭りにちなんだ問題を用意しました。

今回の問題では、基数性については個数を問うています。問題で与えられた集合を認識した上で、落ち着いて数え上げることが必要となります。

また、序数性についてはひな壇を取り上げ、上下左右に関して順番を認識する問題を出題しました。

いきなり紙面上で解くことは難しいため、実際にひな壇を前に、具体的に考えてみるのが良いかと思います。

片付けの際など、是非お子様と一緒にチャレンジしてみて下さいね。

・答①：5人
・答②：6人
・答③：3人
・答④：上から3段目、左から4番目